Les parts més importants de la interfície gràfica de l'applet són les que es troben marcades a la figura:
 
 

Els elements més importants són:
     (a) Pantalla: regió on es visualitzen les ones.
     (b) Velocímetre: scrollbar per controlar la velocitat d'execució.
     (c) Nom del fenomen en execució actualment.
     (d) Botó per interrompre/re-emprendre l'execució.
     (e) Capsa per a l'elecció del tipus de fenomen per visualitzar.
     (f) Botó per canviar de fenomen.
     (g) Opcions: regió on s'escullen els paràmetres de les execucions.

Inicialment, no hi ha cap fenomen en execució. Per escollir-ne un, cal prémer amb el ratolí a (e) i seleccionar una de les opcions. Un cop s'ha decidit quina es vol veure, s'ha de prémer a (f), moment en el qual apareixerà a (g) el conjunt d'opcions corresponents al fenomen escollit. Un cop fixades les variables, s'ha de pitjar al botó "Aplicar" que apareixerà a (g). A (a) començarà llavors l'evolució de les ones. Si en qualsevol moment es vol aturar l'execució, cal pitjar (d), de forma que al botó passarà a dir-hi "Continuar". Per continuar la visualització, s'ha de tornar a prémer aquest mateix botó. Mentre l'execució resti aturada, es podran canviar totes les opcions, la velocitat o la funció escollida, però cal tenir present que la pantalla no canviarà fins que es desinhibeixi l'execució.

Per defecte la velocitat té un valor, però depenent de les característiques de l'ordinador sobre el qual s'executa l'applet l'evolució pot ser bastant lenta o massa ràpida per apreciar bé els fenòmens. És per això pel que serveix la barra (b). Si l'ordinador és lent, es pot pujar el nivell fins a dalt de tot per accelerar la pantalla. És possible que hi hagi ordinadors que tot i admetre el llenguatge Java siguin massa lents com per fer servir aquest applet amb prou velocitat. En canvi, en altres màquines (especialment si es troben poc carregades amb més processos) la velocitat per defecte por ser massa alta, o potser es desitja veure a càmera lenta una determinada situació. Per reduir la velocitat, tot el que s'ha de fer és abaixar el nivell de la barra (b).

Cada fenomen disposa de controls diferents. En general, hi ha dos tipus de paràmetres: continus i discrets. Els primers, nombres reals per la freqüència, amplitud, velocitat d'un medi, etcètera, s'escullen en un camp de text. Cal escriure'n el valor desitjat, fent servir el caràcter '.' per indicar punt decimal. Els discrets, d'altra banda, s'escullen típicament amb checkboxes, pitjant sobre l'opció que es vulgui. Solen tractar-se de dues o tres opcions excloents, de manera que en pitjar en una de elles es canvia l'elecció. L'excepció a aquest comportament és a l'opció de visualització dels modes normals. Es demana un nombre natural, i no real, a un camp de text. S'explicarà ara cada panell d'opcions, amb els límits per a les variables i què representa cadascuna.

Sinusoïdals
Condicions de contorn
Superposicions
Desfasaments de sinusoïdals
Ones estacionàries
Pulsacions
Modes normals
Discontinuïtats de medi
Curiositats a corda
Adaptació de velocitats

SINUSOÏDALS
 

El camp "Freqüència" ha de trobar-se entre 0.2 i 20. Val a dir que les magnituds que es fan servir tant en aquest apartat com en la resta no tenen unitats, i els seus valors són només relatius. La raó d'això és que la velocitat d'execució de les aplicacions en Java és molt dependent de la màquina sobre la qual treballa (i fins i tot del navegador que es faci servir). No es pot dir per tant que la freqüència es troba en hertzos, perquè depenent de l'ordinador (i per suposat també del valor del velocímetre) una freqüència igual a 2 pot correspodre's a 4 o a 0.04 Hz en execució. La interpretació de les freqüències, doncs, es fa a partir de la relació nl=c, n: freqüència, l: longitud d'ona. Si la longitud del fragment d'ona visible a la pantalla és L, i la freqüència escollida és f, llavors el nombre de longitud d'ones que caben a L serà igual a f (o el que és el mateix, , recordant que f no té unitats).
Una cosa similar succeeix amb les amplituds, ja que la funció espacio-temporal que es representa és adimensional. És intranscendent, doncs, si el que es representa té amplitud 1 o 100, gràcies al caràcter lineal de l'equació d'ona. S'ha decidit fer que les ones d'amplitud 1.15 encaixin exactament a la pantalla, però aquesta elecció és absolutament arbitrària.

El camp de l'amplitud admet qualsevol nombre real (sempre que es trobi dins dels límits de la representació que fa servir el llenguatge de programació Java), cosa que inclou els negatius.
Pel que fa al sentit de desplaçament de l'ona, les dues opcions són auto-explicatives. 'dreta' fa que la velocitat de les ones sigui positiva (prenent el conveni que velocitats positives impliquen moviment cap a la dreta de la pantalla), mentre que per 'esquerra' la velocitat té el mateix valor absolut però amb signe oposat.

Com succeirà sempre, les modificacions en els paràmetres no es fan efectives fins que s'apreta "Aplicar". Si els camps de text no contenen nombres amb un format adient (tenen alguna lletra, estan en blanc, més d'un punt decimal, etc.), se'ls assigna el valor per defecte en pitjar el botó. Si es troben per fora dels intervals vàlids, prenen el valor extrem vàlid més pròxim a l'introduït. Aquestes consideracions són igualment aplicables a tots els camps de text de les altres opcions.

Encara que només sigui amb la precisió que ofereix la vista, es pot comprovar que la velocitat de desplaçament de les ones és independent de la seva freqüència, amplitud i sentit. També ha de servir per verificar que el producte entre la longitud d'ona i la freqüència és constant.
 

L'alçada i l'amplada es corresponen a les d'un pols gaussià. Si bé el criteri per interpretar l'alçada dels pols és el mateix que per a l'amplitud en les sinusoïdals (també pot ser negatiu), el camp de l'amplada no té el mateix rang que el de les freqüències dels sinus. Ha de valer entre 2.0 i 12.0, i es tracta de l'amplada característica d'una gaussiana mesurada en unitats de Dx (interval entre dos consecutius en la resolució numèrica). Tot i que amb aquesta definició potser costa fer-se una idea de quant correspon a aquesta mesura, observant algun exemple n'hi ha prou per ajustar-la.
Només pot estar activat un tipus d'extrem, ja sigui 'lliure', 'fix', o 'periòdic', que com els seus noms indiquen fan que els extrems de l'ona siguin, respectivament, lliures, fixats, o hi hagi condicions periòdiques de contorn.

Quan es dóna a "Aplicar", es genera un pols gaussià a l'exterm esquerre de la pantalla, i que es va propagant cap a la dreta. En arribar a l'extrem dret, el seu comportament dependrà del tipus d'extrems escollits. Si és 'lliure', s'hi reflectirà sense canviar la fase. Abans que s'allunyi de l'extrem, el valor de l'ona en els punts propers a ell arriben al doble de magnitud que l'alçada original del pols inicial, perquè com es recordarà hi ha superposició d'ones, en aquest cas del fragment de pols que encara no ha arribat a l'extrem i el que ja s'ha reflectit. Quan el pols arriba a l'exterm esquerre, té lloc una reflexió idèntica, perquè aquest extrem és també lliure.
El que passa quan es troba actiu el tipus d'extrem 'fix' és semblant, amb la diferència que ara hi ha canvi de fase. També es pot observar la superposició del fragment de pols que arriba a l'extrem i el que ja s'hi ha reflectit. L'extrem esquerre serà també fixat, tornant a donar-se reflexió amb canvi de signe.
Amb l'opció de condicions de contorn periòdiques el que s'observarà és que el pols apareix per l'esquerra mentre va desapareixent per la dreta, com a il·lustració de les conseqüències de l'elecció d'aquestes condicions de contorn a l'hora de resoldre problemes físics.
 

L'equació d'ones és lineal, cosa que implica que les seves solucions compleixen el principi de superposició, la visualització del qual es pot fer amb aquest apartat. Per a l'observació de superposicions està aquesta opció, en la qual es poden generar polsos gaussians o quadrats d'amplada, alçada i signe variables.

Els límits per a les amplades i amplituds dels polsos són els mateixos que en l'apartat anterior: entre 2.0 i 12.0 per l'amplada i qualsevol valor per a l'alçada, fin i tot negatius (tot i que, naturalment, si són molt més grans que 1 no cabran a la pantalla). Qualsevol dels dos polsos pot ser quadrat, i les primeres dades són per al pols que parteix de l'esquerra, essent les dades del pols que surt per la dreta les segones.
Un cop es pitja "Aplicar" es generen els dos polsos amb les característiques triades, desplaçant-se l'un cap a l'altre. Es pot apreciar llavors la superposició d'ambdós, i que quan s'allunyen no han perdut la forma original. Després de generar els polsos, els extrems es converteixen en infinits, per la qual cosa desapareixen els polsos en arribar-hi.

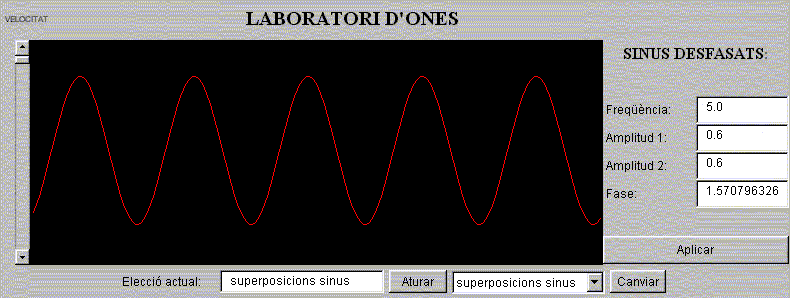
En aquesta ocasió, es té l'oportunitat de veure la superposició de dues sinusoïdals amb la mateixa freqüència, però cadascuna amb una amplitud i desfasades.

Hi ha camps d'edició de text per introduir la freqüència (la mateixa per les dues sinusoïdals), les dues amplituds i la fase. El sentit de moviment no té importància, i per això es generarà per l'esquerra una ona que es desplaci cap a la dreta, i que a l'extrem esquerre valdrà
  f(0,t)=A₁sin(2p Ft) + A₂sin(2pFt + j) , essent F la freqüència elegida, A₁ i A₂ les amplituds i j la fase en radians.
Com sempre, el valor de la freqüència no té unitats, i per tant el temps que apareix a la fórmula anterior tampoc en pot tenir. S'ha de fer una interpretació d'ell en el sentit que s'ha explicat en l'apartat referent a les sinusoïdals. La fase, inicialitzada a p/2, pot assolir qualsevol valor real, encara que naturalment les ones produïdes amb j ₀ i j₀+2pj (j enter) han de ser iguals.
Els casos més característics per analitzar són j=0 i j=p. Per al primer, l'ona generada serà una amb amplitud A₁+A₂ i de freqüència F. En canvi, a l'altre la freqüència tampoc es modifica, però l'amplitud passa a ser A₁-A₂.
A la imatge anterior hi ha la suma de dos sinus desfasats 90º, cosa que fa que l'amplitud resultant no sigui la suma de les inicials per separat.

Les ones estacionàries es donen quan es superposen dues ones sinusoïdals d'igual amplitud i freqüència però que es mouen en sentits oposats. Per veure què passa en aquesta situació, només cal sumar les dues ones,  f₁=Asin (kx-wt) (movent-se cap a x creixents), i f₂=Asin(kx+wt). Fent ús de la igualtat trigonomètrica , la suma d'f₁ i f₂ queda

Es tracta d'un perfil sinusoïdal en l'espai (el terme sin(kx)), l'amplitud del qual en cada instant de temps és 2Acos(wt), o, interpretat d'una altra manera, cada punt vibra amb una freqüència  w en fase amb els altres i amb una amplitud 2Asin(kx). De l'ona resultant se'n diu estacionària.
La forma més simple d'obtenir dues ones d'igual amplitud i freqüència però movent-se en sentits oposats és aprofitant la reflexió que es dóna quan un tren d'ones arriba a un extrem, ja sigui fix o lliure. És així com es generaran aquestes ones en l'aplicació.

Com sempre, els camps del quadre de controls per la freqüència i l'amplitud es refereixen a la sinusoïdals generada, i tenen les mateixes limitacions i interpretacions que en la primera opció. A continuació, es pot seleccionar com es vol que siguin els dos extrems: per l'esquerre, hi ha la possibilitat que sigui forçat o transparent; el dret pot ser lliure o fixat. Quan es prem el botó d'"Aplicar" apareix per l'esquerra (i movent-se cap a la dreta, és clar) un tren sinusoïdal de l'amplitud i freqüència escrites. En arribar a l'extrem dret, es reflectirà, i depenent de com sigui l'exterm canviarà de fase o no (veure l'opció de condicions de contorn). A mesura que el front de l'ona reflectida es va desplaçant cap a l'esquerra es va formant l'ona estacionària.
Si l'extrem esquerre és posat com a 'transparent', l'ona reflectida seguirà avançant cap a l'esquerra indefinidament, a l'hora que per aquest costat segueix arribant una sinusoïdal des de l'infinit, per la qual cosa a la pantalla hi restarà una ona estacionària, suma de de la que ve per l'esquerra més la que ve per la dreta, que es crea amb la reflexió de la primera.
En oposició, si s'ha imposat que l'extrem esquerre sigui forçat, el que es veu és bastant diferent. Que l'extrem sigui forçat vol dir que en ell l'ona sempre val  F(0,t)= Asin(wt) (w, la velocitat angular, és igual a 2p vegades la freqüència). Quan l'ona reflectida inicialment arriba a aquest altre extrem, es reflectirà de nou amb un canvi de fase, perquè és com si arribés a un extrem fixat a F(0, t). El que això provoca és que una nova sinusoïdal es sumi a l'ona estacionària ja formada. Quan l'ona original, que ja ha rebotat a la dreta i a l'esquerra, torni a l'extrem dret, es donarà una nova reflexió. Aquestes reflexions tindran lloc indefinidament.
Com que cada cop que l'ona retorna cap a l'esquerra s'està superposant a una que va cap a la dreta, les ones estacionàries es destrueixen quan el front d'ones va d'esquerra a dreta, però es regeneren quan va al revés. Existiran unes freqüències (que es poden dir de ressonància) per les quals l'amplitud de les ones estacionàries vagi creixent cada dues reflexions, perquè si l'ona estacionària que es té i la generada en amb la reflexió a l'extrem esquerre del front d'ones tenen la mateixa fase temporal, l'amplitud de la superposició d'ambdues serà la suma de les amplituds. En canvi, per altres freqüències (d'anti-ressonància) les dues ones estacionàries per sumar estaran completament desfasades, de manera que la superposició d'elles serà zero.
Els valors d'aquestes freqüències dependran de si l'extrem dret és fix o lliure, perquè hi tindrà lloc un canvi de fase o no. Per al primer tipus d'extrem, els valors de la freqüència de ressonància han de ser números de la forma , i els d'anti-ressonància, (amb n natural). Si l'extrem és lliure, la ressonància hauria de donar-se quan la freqüència és , i l'anti-ressonància amb valors del tipus .

Un altre dels fenòmens que es donen quan es sumen dues ones sinusoïdals és el de les pulsacions. Suposant que es tenen dues ones movent-se en el mateix sentit, però cadascuna amb la seva pròpia freqüència (de moment, es suposarà la mateixa amplitud), f₁=Asin (k₁x-w₁t), i f₂=Asin (k₂x-w₂t), la suma valdrà

Com abans, es pot interpretar el resultat com una ona de freqüència 2p(w₁+ w₂ (i nombre d'ones k₁+k₂) modulada amb una amplitud igual a , que li dóna el característic perfil de pulsacions quan les dues freqüències són molt properes, ja que llavors w₁-w₂ <<w₁+w₂.
Si les dues amplituds no són iguals, es pot re-escriure f₂ =Bsin(k₂x-w₂t)=Asin (k₂x-w₂t)+(B-A)sin k₂x-w₂t). Queda, doncs, un terme addicional a les pulsacions (per amplituds semblants, aquest terme addicional és petit, (A-B)<<A).

Al programa es poden variar les dues freqüències i amplituds (amb els marges de sempre), per observar que les polsacions només es donen quan les freqüències (i les amplituds) són semblants, a més de verificar visualment els valors de les longituds d'ona de les modulacions.

En una corda amb els extrems fixats, es poden generar ones estacionàries, però només es mantindran aquelles que tinguin una longitud d'ona que compleixi l=2L/n, L: longitud de la corda,n: nombre natural, perquè són les úniques que poden tenir els dos extrems sempre fixats a zero. Segons el nombre de mitges longituds d'ona que tingui l'ona dins el segment de corda, es parla del primer, segon, tercer, etc. mode normal.

Les possibilitats d'elecció en aquest fenomen es limiten a la de l'enèsim mode normal per visualitzar. El nombre a introduir ha de ser un natural (1, 2, 3,...). No hi ha cap màxim (més que el de la representació en un ordinador d'un enter), però és clar que per als modes més enllà del desè la qualitat de l'observació no pot serà molt gran. Això passa perquè la freqüència d'oscil·lació és igual a c/l, i l =2L/n (on n és el nombre del mode normal). La freqüència augmenta linealment amb el nombre del mode, per la qual cosa quan el mode és relativament gran la freqüència pot ser massa alta per apreciar bé les oscil·lacions, fins i tot reduint la velocitat d'execució. A més, si la longitud d'ona és molt petita el perfil pot no ser suau (cal no oblidar que es resol numèricament l'equació d'ona).

Quan es té una discontinuïtat en la velocitat de transmissió de les ones (un canvi de medi), un pols que hi arribi es descompon en una part que es transmet al segon medi i una altra que es reflecteix al canvi de medi. El coeficients de transmissió i reflexió (quocient entre l'amplitud del pols transmés i reflectit entre l'amplitud del pols incident) tenen expressions de la forma i , respectivament, essent c₁ i c₂ les velocitats del primer i el segon medis.
En aquesta aplicació es pot veure què passa en aquestes discontinuïtats amb sinusoïdals i polsos gaussians. El canvi de medi es troba al mig de la pantalla, i s'hi dirigeix des de l'extrem esquerre. L'ona reflectida i la transmesa desapareixen en arribar als respectius extrems (continuen fins a l'infinit).
Les velocitats dels medis estan limitades a l'interval [1.0, 4.0]. Tot i que sembli que es tracta d'un interval massa restringit, el índexs de refracció dels medis transparents més usuals rarament superen el valor de 2, cosa que vol dir que la velocitat de transmissió de les ones lluminoses en ells no sol ser més petita que la meitat de la de la llum al buit. En aquesta aplicació, es permeten relacions de fins a la quarta part. Si el que es vol veure és que succeeix quan l'ona passa a un medi amb velocitat més petita que la de l'inicial, només cal posar un valor més gran per a la primera velocitat que per a la segona.
El color del fons de la pantalla indica depèn de la velocitat del medi: com més clara sigui la tonalitat, més gran és la velocitat en el medi.

Amb una tria adequada de velocitats, es pot veure que l'amplitud de l'ona transmesa pot ser més gran que la de la incident, i que la reflexió pot comportar canvi de signe o no (veure els coeficients de transmissió i reflexió).

Aquesta opció simplement es troba per mostrar alguns exemples de l'evolució de determinades ones amb condicions inicials diverses, situades entre dos extrems fixats, com seria el cas de pertorbar una corda elàstica amb els extrems fixats.
Els exemples disponibles són:

• 'Estirat centre': Es parteix d'una situació en la qual es tiba la corda pel punt mig, quedant estirada amb pendent constant a banda i banda, trobant-se una discontinuïtat en la derivada al punt central. Llavors es deixa anar.
• 'Estirat descentrat': Aquest exemple és similar, però ara no s'estira pel punt mig sinó per un de desplaçat, obtenint-se una evolució lleugerament diferent.
• 'Gaussiana': De l'observació del primer mode normal es pot arribar erròniament a la idea que qualsevol perfil inicialment en repòs vibra estacionàriament. Com a exemple per veure que no és així, es presenta una condició inicial on la corda assoleix un perfil gaussià i els punts no es mouen per t=0. Un cop es deixa anar, el que es veu és que, en realitat, el perfil inicial era una superposició de dos polsos gaussians, movent-se cadascun en un sentit.
• 'Sinus al quadrat': s'inicialitzen els punts amb f(x,0)=sin2 (5px/L), i , i es deixa evolucionar.
• 'Fragment sinusoïdal': Similar a l'anterior, es té un fragment de corda inicialitzat com si es tractés d'un mode normal, però la resta és a zero.
• 'Velocitat inicial': Tots els exemples anteriors partien d'una situació estàtica (). Com a mostra d'unes condicions inicials diferents, en aquest cas es té f(x, 0)=0 i .

Tots aquests casos es troben per ensenyar situacions no gaire habituals, i la majoria d'ells són difícilment realitzables en la pràctica (no sol ser possible fixar les condicions inicials tan lliurement). Es pot demostrar, però, que mitjançant desenvolupaments en sèrie de Fourier tota ona en un segment amb els extrems fixats pot ser descomposta en suma ponderada (potser infinita) de modes normals. Pot ser interessant intentar trobar els coeficients dels termes de Fourier de la sèrie a partir de les condicions inicials de cada exemple, i després fer la sumar per a un temps t, verificant que realment el perfil és el mateix que l'obtingut amb la resolució numèrica de l'equació d'ona. En general no és gens difícil calcular els coeficients de la sèrie, però esdevé molt costós (o impossible) fer-ne després la suma analíticament. Es pot obtar, però, per sumar amb l'ajut d'algun programa d'ordinador un nombre finit (però prou gran) de termes, traient una sortida gràfica, i comparar llavors els resultats d'ambdós programes. Cal dir que aquest procediment pot quedar fora de l'abast i els objectius dels estudiants amb coneixements no molt avançats.

Les discontinuïtats en la velocitat de transmissió produeixen efectes indesitjables, com que l'amplitud de les ones transmeses sigui diferent de la de les incidents, o que una ona s'hi reflecteixi parcialment. Donats dos medis amb velocitats diferents, seria important trobar algun mètode per reduir la importància de les reflexions i canvis d'amplitud.
Quan es passa a un medi amb velocitat més petita que la de l'inicial, el coeficient de transmissió és més petit que 1. Es pot comprovar que si s'introdueix un altre medi entre els originals, el coeficient de transmissió del sistema format pels dos medis és més gran que el del conjunt sense l'intermedi si la velocitat de transmissió d'aquest nou medi es troba entre les dues primeres velocitats (fent-ne la composició, i dient c₁, c₂ i c₃ a les velocitats de cadascun dels medis, essent c₁ > c₂ > c₃, el coeficient de transmissió final és

.

En aquesta opció es poden visualitzar les conseqüències d'una o altra elecció. A més de poder escollir les velocitats dels medis inicial i final (com abans, han de comprendre's entre 1.0 i 4.0), es pot triar si l'adaptació es fa amb un únic medi o amb un continu. El camp on s'introdueix la velocitat del segon medi és ignorat si es selecciona la segona opció. És important aclarir que tot i que es diu a l'opció 'gradació progressiva', en realitat l'adaptació es porta a terme amb l'interposició d'una certa quantitat de medis amb velocitat constant, de forma que la diferència entre les velocitats de dos medis contigus sigui molt petita. No es pot oblidar que el programa calcula una solució numèrica, i que per tant no es pot aconseguir que les variacions siguin contínues, donat que s'ha de discretitzar tot. Per tant, la gradació no és estrictament contínua, i els resultats variaran lleugerament de la solució real.
Una vegada fixats els paràmetres, només queda pitjar "Aplicar". Es genera un pols gaussià per l'esquerra, i se'n veu l'evolució. És bo ser conscient que posant un medi intermig l'amplitud del pols final és lleugerament més gran que la que s'obté sense ell (es pot comparar amb el que surt a l'apartat de dos medis), però que no es poden evitar les reflexions, que distorsionen el senyal. Quan la gradació és suau, l'ona que torna cap a l'esquerra és molt més petita, però les interferències de les petites reflexions que es donen en cada regió de canvi de medi no es poden eliminar. A més, el pols final segueix sent de diferent magnitud que l'inicial.