Si deseamos conocer el campo eléctrico en el punto producido por cargas puntuales en las posiciones fijas. Sabemos quesatisface el principio de superposición, que se expresa como:

donde es la localización fija de la carga i-ésima y es una constante que depende las unidades escogidas. En el S.I. (Sistema Internacional) de unidades, la carga se mide con Coulombs (C) y la constante K viene dada como:

La constante es la permitividad eléctrica del vacío. Esta selección no es muy conveniente para el cálculo con ordenador ya que >>1. Otro sistema de unidades es el Gaussiano (cgs), para el cual, la constante es absorbida dentro de la unidad de carga, con lo que . La carga se expresa pues en unidades electrostáticas o "esu". En este sistema los campos eléctricos y magnéticos tienen las mismas unidades. Por ejemplo, la fuerza sobre una partícula con carga y velocidad que se mueve dentro de una zona con un campo eléctricoy un campo magnético, se expresa :

Estas características del sistema Gaussiano de unidades nos inducen a adoptarlo como sistema de unidades para realizar nuestra aplicación. La manera habitual utilizada para visualizar campos eléctricos es dibujar las líneas del campo eléctrico. Las propiedades de dichas líneas son las siguientes:

• Una línea de campo eléctrico es una línea tal que la tangente a la misma, en cualquier punto, es paralela al campo eléctrico existente en esa posición.

• Las líneas son uniformes y continuas con origen en las cargas positivas y final en las negativas.

• La densidad de líneas en un punto cualquiera del espacio es proporcional a la magnitud del campo en ese punto. Esta propiedad implica que el número total de líneas del campo eléctrico desde un punto con carga es proporcional a la magnitud de esa carga.

La aplicación dibuja las líneas de campo eléctrico comenzando por las cargas positivas si , o por las cargas negativas si . El programa implementa el siguiente algoritmo:

1. Comienza en un punto cerca de una carga y computa las componentes del vector del campo eléctrico en ese punto usando la primera fórmula descrita.
2. Se dibuja un pequeño segmento de línea de medida tangente a en ese punto. Si entonces , de otro modo . Las componentes del segmento de línea vienen dados como:

 

 



 

El programa usa un D s pequeño si la línea de campo está cerca de las cargas o si la magnitud del campo es grande. Con el objetivo de acelerar el programa, se utiliza un valor grande para D s cuando una línea de campo se mueve fuera de la pantalla y la magnitud del campo es pequeña.

3. El proceso se repite desde el principio a partir del punto, y continúa hasta que la línea de campo se aproxima a otra carga.
4. Los pasos 1,2 y 3 se repiten para puntos equidistantes en un círculo alrededor de la carga, donde la distancia es inversamente proporcional a la magnitud de la carga.
5. Se repetirá para cada una de las cargas del mismo signo los pasos 1,2,3 y 4.

FUNDAMENTOS FÍSICOS DE LAS GUÍAS DE ONDAS

El mundo de las comunicaciones está basado en la transmisión de información mediante ondas electromagnéticas (OEM) entre un emisor y un receptor. Fundamentalmente podemos dividir esta transmisión en dos tipos fundamentales:

• A través de un cable o guía de ondas (GdO).

• Radiación de OEM a través del aire, el espacio libre o de un medio dieléctrico.

La búsqueda de canales con baja atenuación y la necesidad de enviar señales con un ancho de banda cada vez mayor ha hecho que las GdO, que son el objeto de estudio de este proyecto, jueguen un papel cada vez más importante en del conjunto de medios físicos para la comunicación. La televisión por cable, la telefonía, Internet, etc. obligan a un uso cada vez mayor de GdO, en particular de fibras ópticas.

Se llama GdO a cualquier estructura, o parte de una estructura, que hace que una OEM se propague en una dirección determinada, con algún grado de confinamiento en el plano transversal a la dirección de propagación. El guiado de las ondas se consigue debido a la conexión entre los campos y las cargas o corrientes en los contornos o bien por condiciones de reflexión en los límites. Su origen se sitúa en los años 30 cuando se empezaron a utilizar en radares y emisoras de radio de frecuencias de microondas.

La estructura y el material de construcción de les GdO depende de la frecuencia de les ondas que deben transportar. Para frecuencias del orden de las microondas son habitualmente sistemas abiertos o cerrados de conductores metálicos. A frecuencias ópticas se utilizan GdO dieléctricas.

Todas ellas presentan la característica común de que, si la frecuencia es suficientemente alta, diversas configuraciones de los campos eléctrico y magnético (los llamados modos) se pueden propagar en la misma guía simultáneamente, aunque con diferentes velocidades. La estructura de estos modos es a menudo bastante complicada y difícil de visualizar debido a su estructura tridimensional.

El objetivo de este proyecto es precisamente la visualización gráfica de estos modos para una guía de ondas rectangular de paredes conductoras.

Es necesario comentar también que todas las GdO tienen una frecuencia de corte por debajo de la cual la transmisión es imposible. Esta frecuencia es inversamente proporcional a la dimensión transversal de la guía. Esto produce que sean factibles para la transmisión de señales de frecuencias a partir de 1GHz (microondas) ya que a frecuencias menores requerirían unas dimensiones demasiado grandes.

La GdO rectangular de paredes conductoras es la más importante de les GdO en forma de tubo. Consideramos una región dieléctrica de ancho a y altura b que se estiende indefinidamente en la dirección axial (z) y que está totalmente cerrada por paredes conductoras.

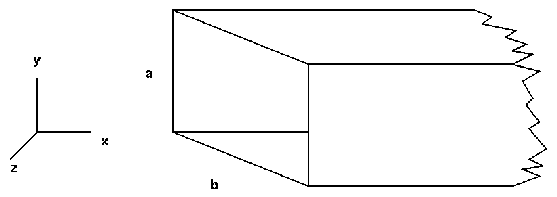
Con el objetivo de encontrar los modos de la GdO se tiene que encontrar la solución de las ecuaciones de Maxwell bajo las condiciones de contorno impuestas por las características de la guía. Se supone que la región dieléctrica limitada por los conductores no tiene pérdidas y por tanto la densidad de corriente eléctrico en el su interior es nula, . La dependencia en la posición y el tiempo de los campos que consideramos es:

donde usamos la habitual notación compleja y el superíndice + (-) indica una OEM que se propaga en el sentido positivo (negativo) del eje z.

Las ecuaciones de Maxwell que gobernaran el comportamiento de las ondas son:

donde son respectivamente el campo eléctrico, el vector de inducción magnética, el campo magnético y el desplazamiento eléctrico. A partir de estas ecuaciones se llega a las ecuaciones de onda vectoriales:

donde son la permisividad eléctrica y la permeabilidad magnética del medio dieléctrico, respectivamente.

Las soluciones de estas ecuaciones se pueden descomponer en clases que reciben el nombre de modos y que pueden ser, en general, de los siguientes tipos:

• Modos transversales magnéticos (TM) en los cuales .

• Modos transversales eléctricos (TE) en los cuales .

• Modos transversales electromagnéticos (TEM) en las que tanto como .

En las GdO vacías como las que estudiaremos aquí se puede demostrar que no existen los modos TEM, que per otra parte son los dominantes en los sistemas de dos conductores, como los cables coaxiales.